목차
1. 문제 설명
2. 정답
1. 문제 설명
https://www.acmicpc.net/problem/12865

정말 말그대로 평범한 배낭 알고리즘 문제로, 점화식을 도출하는 방법을 정리해보려고 한다.
배낭 알고리즘은 전형적인 dp문제다.
결국에 배낭에 물건을 담냐, 담지 않느냐로 쪼갤 수 있기 때문이다.
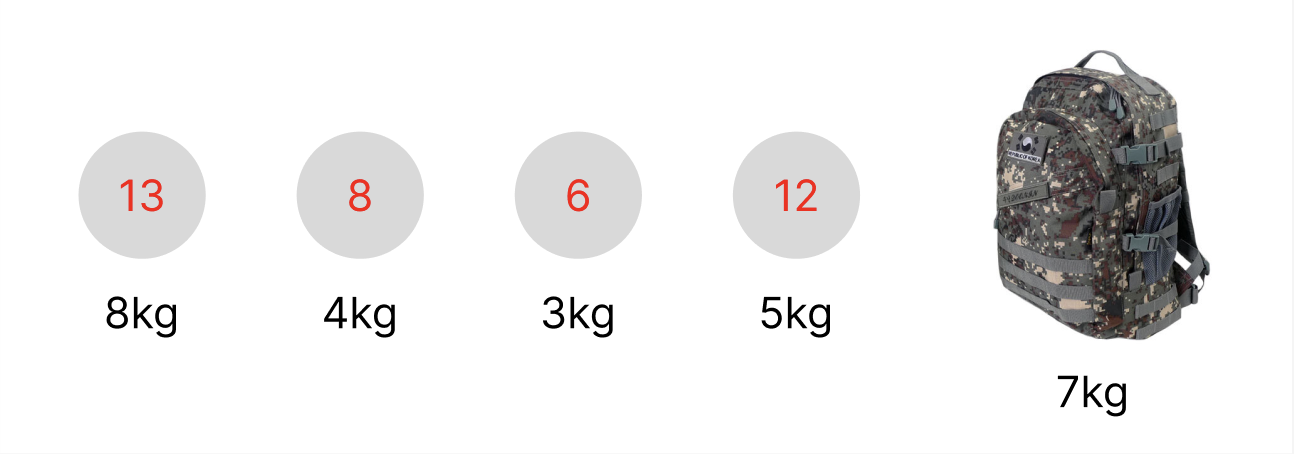
먼저 dp 배열을 정의해보자.
dp[i][w]
- i번째까지의 물건을 고려했을 때
- 무게 w를 버틸 수 있는 배낭의 최대 가치
물건을 선택할 때에는 두 가지 선택지가 있다.
1. 현재 물건의 무게가 배낭에 담을 수 있는 최대 무게를 초과
첫 번째 물건의 무게는 8kg로 배낭에 최대로 담을 수 있는 무게인 7kg를 초과한다.
이 경우, 배낭에 물건을 담을 수 없다.
따라서 이전 상태의 값을 그대로 가져온다.
점화식은 아래와 같다.
dp[i][w] = dp[i - 1][w]
2. 현재 물건의 무게가 배낭에 담을 수 있는 최대 무게 이하
두 번째 물건의 무게는 4kg로 배낭에 최대로 담을 수 있는 무게인 7kg 이하다.
이 경우, 다시 두 가지 선택지가 있다.
① 배낭에 물건을 담지 않는다.
② 배낭에 물건을 담는다.
따라서 두 가지 경우에 대한 결과를 각각 구하고 더 큰 값을 취하면 된다.
① 배낭에 물건을 담지 않는다.
배낭에 물건을 담지 않는 경우는 1번과 동일하다.
dp[i][w] = dp[i - 1][w]
② 배낭에 물건을 담는다.
배낭에 최대로 담을 수 있는 무게는 7kg로 정해져있다.
현재 물건(4kg, 가치 8)을 무조건 배낭에 넣었을 때 최대 가치는 현재 물건의 가치 + dp[0][7kg - 4kg]와 같다.
이를 점화식으로 표현하면
dp[i][w] = i번째 물건의 가치 + dp[i - 1][w - (i번째 물건의 무게)] 이다.
배낭에 물건을 담지 않는 경우, 배낭에 물건을 담는 경우에 대한 결과를 각각 구했다면 이제 둘 중 더 큰 값을 할당해주면 된다. 현재 물건의 무게가 배낭에 담을 수 있는 최대 무게 이하인 경우 최종 점화식은 다음과 같다.
dp[i][w] = Math.max(dp[i][w] = dp[i - 1][w], i번째 물건의 가치 + dp[i - 1][w - (i번째 물건의 무게)])
.
.
.
💡 마지막으로 최종 정리하자면 💡
1. 현재 물건의 무게가 배낭에 담을 수 있는 최대 무게 초과
dp[i][w] = dp[i - 1][w]
2. 현재 물건의 무게가 배낭에 담을 수 있는 최대 무게 이하
dp[i][w] = Math.max(dp[i][w] = dp[i - 1][w], i번째 물건의 가치 + dp[i - 1][w - (i번째 물건의 무게)])
2. 정답
import java.util.*;
import java.io.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] input = br.readLine().split(" ");
int N = Integer.parseInt(input[0]); // 물건의 개수
int K = Integer.parseInt(input[1]); // 준서가 버틸 수 있는 무게
int[][] item = new int[N][2]; // 물건 정보
int[][] dp = new int[N][K + 1]; // 가방의 최대 무게가 K, 인덱스 N번까지 봤을 때의 최대 가치
for(int i = 0; i < N; i++) {
String[] info = br.readLine().split(" ");
item[i][0] = Integer.parseInt(info[0]); // 물건의 무게
item[i][1] = Integer.parseInt(info[1]); // 물건의 가치
}
for(int i = 0; i < N; i++) {
for(int j = 0; j < K + 1; j++) {
// 1. 물건이 가방 무게 초과 (담지 않음)
if(item[i][0] > j) {
dp[i][j] = (i == 0) ? 0 : dp[i-1][j];
}
// 2. 물건이 가방 무게 이하
if(item[i][0] <= j) {
// 담는다, 담지 않는다 2가지 선택지 가능 -> 둘 중 큰 걸 선택
// 담는다 = dp[i - 1][j - (i 무게)] + i의 가치
int notSelected = (i == 0) ? 0 : dp[i - 1][j]; // 담지 않는다
int selected = (i == 0) ? item[i][1] : dp[i - 1][j - item[i][0]] + item[i][1]; // 담는다
dp[i][j] = Math.max(selected, notSelected);
}
}
}
System.out.print(dp[N-1][K]);
}
}
'Problem Solving > BOJ' 카테고리의 다른 글
| [Algorithm] 1027 - 고층 건물 (0) | 2025.09.22 |
|---|---|
| [Algorithm] 5052 - 전화번호 목록 (0) | 2025.09.08 |
| [Algorithm] 1197 - 최소 스패닝 트리 (0) | 2025.09.03 |
| [Algorithm] 1138 - 한 줄로 서기 (1) | 2025.09.01 |
| [Algorithm] 2146 - 다리만들기 문제 풀이 (1) | 2025.03.10 |
